Pecahan adalah salah satu konsep matematika yang sering digunakan dalam kehidupan sehari-hari. Anda mungkin sering menemui pecahan ketika berbelanja, memasak, atau bahkan dalam pembagian tugas. Meskipun pecahan dapat menjadi sesuatu yang membingungkan bagi beberapa orang, kalkulator pecahan dapat menjadi teman setia dalam menghitung dan menyederhanakan bilangan pecahan. Dalam artikel ini, kita akan menjelaskan apa itu pecahan, mengapa kita perlu kalkulator pecahan, dan bagaimana cara menggunakannya.
Pecahan adalah konsep penting dalam matematika, dan kalkulator pecahan adalah alat yang sangat berguna dalam menghitung, menyederhanakan, dan mengonversi pecahan. Dengan menggunakan kalkulator pecahan, Anda dapat meningkatkan akurasi perhitungan Anda dan menghemat waktu dalam berbagai situasi. Jadi, jangan ragu untuk mengandalkan kalkulator pecahan sebagai teman setia Anda dalam dunia pecahan.
Apa Itu Pecahan?
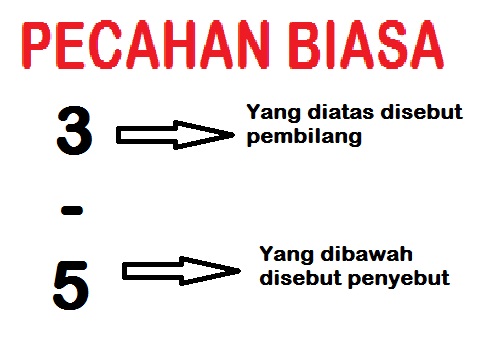
Pecahan adalah representasi dari suatu bilangan yang dinyatakan dalam bentuk perbandingan antara pembilang (angka di atas) dan penyebut (angka di bawah). Sebuah pecahan umumnya ditulis dalam format “a/b,” di mana ‘a’ adalah pembilang dan ‘b’ adalah penyebut. Contohnya, 1/2, 3/4, atau 5/8.
Pecahan digunakan untuk menyatakan bagian dari suatu bilangan bulat. Misalnya, 1/2 berarti setengah dari satu keseluruhan, 3/4 berarti tiga perempat dari satu keseluruhan, dan seterusnya.
Mengapa Kita Memerlukan Kalkulator Pecahan?
Kalkulator pecahan adalah alat yang sangat berguna untuk mempermudah perhitungan dan penyederhanaan pecahan. Berikut beberapa alasan mengapa kalkulator pecahan sangat penting:
- Akurasi: Menghitung pecahan secara manual dapat menjadi rumit dan berisiko kesalahan. Kalkulator pecahan membantu memastikan akurasi perhitungan.
- Kecepatan: Pecahan bisa memakan waktu jika dihitung secara manual, terutama jika angka-angka yang harus dioperasikan besar. Kalkulator pecahan dapat menghemat waktu.
- Penyederhanaan: Kalkulator pecahan dapat dengan cepat menyederhanakan pecahan menjadi bentuk paling sederhana. Misalnya, 4/8 akan disederhanakan menjadi 1/2.
- Konversi: Kalkulator pecahan juga memungkinkan Anda mengonversi pecahan ke desimal dan sebaliknya. Hal ini sering diperlukan dalam berbagai konteks matematika.
- Penggunaan Sehari-Hari: Dalam kehidupan sehari-hari, Anda mungkin perlu menghitung pecahan saat memasak, berbelanja, atau berbagi sesuatu. Kalkulator pecahan dapat sangat membantu.
Cara Menggunakan Kalkulator Pecahan
Menggunakan kalkulator pecahan umumnya sangat mudah. Berikut langkah-langkah umum dalam menggunakannya:
- Masukkan Pecahan: Ketik pecahan Anda ke dalam kalkulator pecahan. Biasanya, Anda akan memasukkan pembilang dan penyebut secara terpisah.
- Pilih Operasi: Pilih operasi matematika yang ingin Anda lakukan, seperti penambahan, pengurangan, perkalian, atau pembagian.
- Hasil: Kalkulator pecahan akan memberikan hasil dalam bentuk pecahan atau desimal, tergantung pada preferensi Anda.
- Penyederhanaan: Kalkulator pecahan seringkali memiliki opsi untuk menyederhanakan hasil ke bentuk yang paling sederhana.
- Konversi (Opsional): Jika perlu, Anda juga dapat menggunakan kalkulator pecahan untuk mengonversi pecahan ke desimal atau sebaliknya.
Hal hal yang harus anda pahami adalah
Pada pecahan, baik dalam bentuk pecahan biasa maupun pecahan campuran, terdapat dua komponen utama: pembilang (numeratir) dan penyebut (denominator). Inilah penjelasan kedua komponen tersebut:
1.Pembilang (Numerator):
- Pembilang adalah bagian atas dari suatu pecahan. Ini mewakili jumlah bagian yang ingin Anda hitung atau sebutkan.
- Pembilang menunjukkan seberapa banyak bagian dari keseluruhan yang sedang diwakili oleh pecahan tersebut.
- Dalam pecahan biasa, pembilang adalah bilangan di atas garis pecahan (misalnya, dalam 3/4, 3 adalah pembilang).
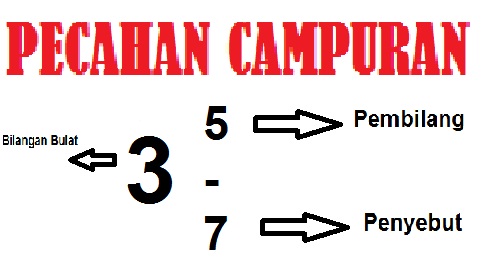
- Dalam pecahan campuran, pembilang adalah bilangan yang merupakan pecahan yang ada setelah bilangan bulat (misalnya, dalam 2_3/4, 3 adalah pembilang).
2.Penyebut (Denominator):
- Penyebut adalah bagian bawah dari suatu pecahan. Ini menunjukkan jumlah total bagian dalam satu keseluruhan.
- Penyebut adalah angka di bawah garis pecahan.
- Dalam pecahan biasa, penyebut adalah bilangan di bawah garis pecahan (misalnya, dalam 3/4, 4 adalah penyebut).
- Dalam pecahan campuran, penyebut adalah bilangan yang ada setelah garis bawah pada bilangan campuran (misalnya, dalam 2_3/4, 4 adalah penyebut).
Jadi, dalam konteks pecahan, pembilang memberi tahu Anda seberapa banyak bagian yang diambil atau dihitung, sedangkan penyebut memberi tahu Anda total jumlah bagian yang ada dalam satu keseluruhan. Misalnya, dalam pecahan 3/4, “3” adalah pembilang yang menunjukkan bahwa kita mengambil tiga bagian dari empat bagian yang ada sebagai keseluruhan.
Kalkulator Pecahan Biasa
Kalkulator Pecahan Campuran
Kalkulator Pecahan dalam Kehidupan Sehari-hari
Selain digunakan dalam konteks akademis, kalkulator pecahan juga sangat berguna dalam kehidupan sehari-hari. Berikut beberapa contoh penggunaan kalkulator pecahan:
- Memasak
Dalam memasak, seringkali kita harus mengukur dan menyederhanakan bahan makanan dalam bentuk pecahan. Misalnya, jika sebuah resep membutuhkan 3/4 cangkir gula, kalkulator pecahan akan membantu Anda mengukur dengan akurat. Selain itu, dalam merubah resep berdasarkan jumlah porsi yang berbeda, kalkulator pecahan akan memudahkan penyesuaian jumlah bahan.
- Berbelanja
Ketika berbelanja, Anda mungkin menemui harga barang dalam bentuk pecahan, seperti harga diskon 25%. Dengan kalkulator pecahan, Anda dapat dengan cepat menghitung potongan harga atau membandingkan harga per unit untuk memilih yang terbaik.
- Konstruksi dan Renovasi
Dalam proyek konstruksi atau renovasi rumah, pengukuran dalam bentuk pecahan adalah hal yang umum. Kalkulator pecahan akan membantu para pekerja konstruksi untuk menghitung bahan yang dibutuhkan dan memotong bahan dengan presisi.
- Bagi Hasil
Dalam beberapa situasi, Anda mungkin perlu berbagi sesuatu dengan teman atau rekan kerja, seperti hasil penjualan atau keuntungan. Kalkulator pecahan akan membantu Anda membagi secara adil dengan membagi hasil dalam bentuk pecahan yang sesuai.
- Keuangan Pribadi
Dalam pengaturan keuangan pribadi, kalkulator pecahan dapat digunakan untuk menghitung suku bunga, cicilan pinjaman, atau pengeluaran bulanan. Ini memudahkan Anda dalam merencanakan anggaran keuangan Anda.
- Pendidikan
Kalkulator pecahan adalah alat yang sangat berguna untuk siswa yang sedang mempelajari konsep pecahan. Ini dapat membantu siswa memahami operasi pecahan, menyederhanakan pecahan, dan menyelesaikan latihan matematika dengan cepat.
Memahami Pecahan Campuran: Gabungan Bilangan Bulat dan Pecahan
Pecahan campuran adalah konsep matematika yang menggabungkan bilangan bulat dan pecahan menjadi satu bentuk yang lebih komprehensif. Dalam artikel ini, kita akan membahas apa itu pecahan campuran, bagaimana cara mengonversinya ke bentuk pecahan biasa atau desimal, dan bagaimana menggunakannya dalam situasi kehidupan sehari-hari.
Apa Itu Pecahan Campuran?
Pecahan campuran adalah representasi dari suatu bilangan yang terdiri dari bilangan bulat dan pecahan. Bentuk umum dari pecahan campuran adalah a_b/c, di mana:
- ‘a’ adalah bilangan bulat.
- ‘b’ adalah pembilang pecahan.
- ‘c’ adalah penyebut pecahan.
Sebagai contoh, pecahan campuran 2_1/4 berarti “dua dan satu perempat.” Ini mengindikasikan bahwa kita memiliki dua bilangan bulat dan satu perempat dari bilangan bulat ketiga. Pecahan campuran adalah cara yang nyaman untuk menyajikan bilangan dalam situasi di mana kita perlu memadukan bilangan bulat dan pecahan.
Mengonversi Pecahan Campuran
Dalam beberapa kasus, kita mungkin perlu mengonversi pecahan campuran ke bentuk pecahan biasa atau desimal. Untuk melakukannya, kita harus mengikuti langkah-langkah berikut:
- Ubah Bilangan Bulat menjadi Pecahan
Langkah pertama adalah mengubah bilangan bulat menjadi pecahan dengan penyebut yang sesuai. Misalnya, bilangan bulat 2 dapat diubah menjadi pecahan dengan penyebut 1, sehingga menjadi 2/1.
- Gabungkan Pecahan dengan Bilangan Bulat
Selanjutnya, gabungkan pecahan yang dihasilkan dari bilangan bulat dengan pecahan yang sudah ada dalam pecahan campuran. Untuk contoh 2_1/4, kita akan menjumlahkan 2/1 dengan 1/4.
- Sederhanakan (Opsional)
Jika diperlukan, Anda dapat menyederhanakan pecahan yang diperoleh dengan menghilangkan faktor bersama dari pembilang dan penyebut.
- Hasil Akhir
Hasilnya adalah pecahan biasa atau desimal, tergantung pada kebutuhan Anda.
Mengapa Kita Memerlukan Pecahan Campuran?
Pecahan campuran sangat berguna dalam konteks praktis, terutama ketika kita berurusan dengan pengukuran dan perhitungan dalam kehidupan sehari-hari. Beberapa alasan mengapa kita memerlukan pecahan campuran adalah sebagai berikut:
- Pengukuran
Dalam kehidupan sehari-hari, kita sering mengukur barang-barang dalam bentuk pecahan campuran. Misalnya, panjang selembar kertas bisa diukur sebagai 8_1/2 inci, yang berarti delapan inci dan setengah.
- Ilmu Pengetahuan
Dalam ilmu pengetahuan, khususnya fisika dan kimia, pecahan campuran sering digunakan untuk mengukur dan menjelaskan perbandingan berbagai zat.
- Konstruksi
Dalam proyek konstruksi atau renovasi rumah, pecahan campuran digunakan untuk menggambarkan ukuran bahan bangunan seperti kayu atau pipa.
- Pembagian Hasil
Dalam situasi seperti pembagian keuntungan atau tugas dalam bisnis, pecahan campuran dapat digunakan untuk membagi sumber daya dengan jelas.
Pemanfaatan Pecahan Campuran
Dalam kehidupan sehari-hari, kita sering menemui pecahan campuran dalam berbagai konteks, termasuk memasak, berbelanja, membagi keuntungan, atau mengukur benda. Pemahaman yang baik tentang pecahan campuran membantu kita menjadi lebih cermat dan efisien dalam mengelola tugas-tugas sehari-hari yang melibatkan bilangan bulat dan pecahan. Sebagai tambahan, kalkulator atau perangkat lunak matematika dapat membantu dalam mengonversi dan menghitung dengan pecahan campuran.
CONTOH SOAL PECAHAN BIASA
Tentu, berikut contoh soal pecahan biasa beserta solusi jawabannya:
Contoh Soal 1: Penjumlahan Pecahan
Hitung hasil dari penjumlahan berikut:
- 2/3 + 1/4
Solusi Soal 1: Untuk menjumlahkan pecahan, kita harus memiliki penyebut yang sama. Dalam hal ini, kita harus mencari kelipatan persekutuan terkecil (KPK) dari 3 dan 4, yang adalah 12. Kemudian, kita menyesuaikan kedua pecahan ke penyebut 12:
- (2/3) * (4/4) = 8/12
- (1/4) * (3/3) = 3/12
Sekarang, kita dapat menjumlahkan pecahan tersebut:
- 8/12 + 3/12 = 11/12
Jadi, hasil penjumlahan 2/3 dan 1/4 adalah 11/12.
Contoh Soal 2: Pengurangan Pecahan
Hitung hasil dari pengurangan berikut:
- 5/6 – 1/3
Solusi Soal 2: Dalam pengurangan pecahan, kita juga memerlukan penyebut yang sama. KPK dari 6 dan 3 adalah 6, jadi kita akan menyesuaikan kedua pecahan ke penyebut 6:
- (5/6) * (1/1) = 5/6
- (1/3) * (2/2) = 2/6
Sekarang kita dapat mengurangkan pecahan tersebut:
- 5/6 – 2/6 = 3/6
Selanjutnya, kita dapat menyederhanakan pecahan tersebut:
- 3/6 = 1/2
Jadi, hasil pengurangan 5/6 dan 1/3 adalah 1/2.
Contoh Soal 3: Perkalian Pecahan
Hitung hasil dari perkalian berikut:
- 2/5 * 3/8
Solusi Soal 3: Untuk mengalikan pecahan, kita hanya perlu mengalikan pembilang dengan pembilang dan penyebut dengan penyebut:
- (2/5) * (3/8) = (2 * 3) / (5 * 8) = 6/40
Kemudian, kita bisa menyederhanakan pecahan tersebut dengan membagi pembilang dan penyebut oleh faktor bersama terbesar (FPB), yaitu 2:
- (6/40) ÷ 2 = 3/20
Jadi, hasil perkalian 2/5 dan 3/8 adalah 3/20.
Contoh Soal 4: Pembagian Pecahan
Hitung hasil dari pembagian berikut:
- 3/4 ÷ 1/2
Solusi Soal 4: Untuk membagi pecahan, kita perlu mengalikan pecahan pertama dengan kebalikan (pembalik) dari pecahan kedua. Pembalikan dari 1/2 adalah 2/1. Jadi, kita dapat menuliskan perhitungan sebagai berikut:
- (3/4) ÷ (1/2) = (3/4) * (2/1)
Kemudian, kita hanya perlu mengalikan pembilang dengan pembilang dan penyebut dengan penyebut:
- (3/4) * (2/1) = (3 * 2) / (4 * 1) = 6/4
Selanjutnya, kita dapat menyederhanakan pecahan ini dengan membagi pembilang dan penyebut oleh faktor bersama terbesar (FPB), yaitu 2:
- (6/4) ÷ 2 = 3/2
Jadi, hasil pembagian 3/4 oleh 1/2 adalah 3/2.
Contoh Soal 5: Menyederhanakan Pecahan
Sederhanakan pecahan berikut ke bentuk paling sederhana:
- 10/20
Solusi Soal 5: Untuk menyederhanakan pecahan, kita perlu mencari faktor bersama terbesar (FPB) antara pembilang dan penyebut. Dalam kasus ini, FPB dari 10 dan 20 adalah 10. Kita kemudian membagi pembilang dan penyebut oleh FPB tersebut:
- (10/20) ÷ 10 = 1/2
Jadi, hasil penyederhanaan 10/20 adalah 1/2.
Contoh Soal 6: Konversi ke Desimal
Konversikan pecahan berikut ke bentuk desimal:
- 3/8
Solusi Soal 6: Untuk mengonversi pecahan ke desimal, kita cukup membagi pembilang oleh penyebut:
- 3 ÷ 8 = 0.375
Jadi, 3/8 dalam bentuk desimal adalah 0.375.
Contoh Soal 7: Penjumlahan Campuran Pecahan
Hitung hasil dari penjumlahan pecahan campuran berikut:
- 1_2/3 + 2_1/4
Solusi Soal 7: Dalam hal ini, kita perlu menjumlahkan bilangan bulat dan pecahan terlebih dahulu. Kemudian, kita dapat menambahkan pecahan tersebut.
- Bilangan bulat: 1 + 2 = 3
- Pecahan: (2/3) + (1/4)
Untuk menjumlahkan pecahan, kita perlu mencari penyebut yang sama, yang dalam hal ini adalah 12. Kemudian, kita menyesuaikan kedua pecahan ke penyebut 12:
- (2/3) * (4/4) = 8/12
- (1/4) * (3/3) = 3/12
Sekarang kita dapat menjumlahkan pecahan tersebut:
- (8/12) + (3/12) = 11/12
Jadi, hasil penjumlahan 1_2/3 dan 2_1/4 adalah 3_11/12.
Contoh Soal 8: Perbandingan Pecahan
Tentukan pecahan yang lebih besar:
- 3/5 atau 4/7
Solusi Soal 8: Untuk menentukan pecahan yang lebih besar, kita dapat mencari nilai desimal dari masing-masing pecahan dan membandingkannya. Pecahan yang memiliki nilai desimal lebih besar adalah yang lebih besar.
- 3/5 = 0.6
- 4/7 = 0.571428571…
Jadi, 3/5 lebih besar daripada 4/7.
Contoh Soal 9: Penjumlahan Campuran Pecahan dan Pecahan Biasa
Hitung hasil dari penjumlahan berikut:
- 2_1/2 + 3/4
Solusi Soal 9: Dalam hal ini, kita perlu menjumlahkan bilangan bulat dan pecahan terlebih dahulu. Kemudian, kita dapat menambahkan pecahan tersebut.
- Bilangan bulat: 2 + 0 = 2
- Pecahan campuran: 1/2 + 3/4
Untuk menjumlahkan pecahan, kita perlu mencari penyebut yang sama, yang dalam hal ini adalah 4. Kemudian, kita menyesuaikan kedua pecahan ke penyebut 4:
- (1/2) * (2/2) = 2/4
- (3/4) * (1/1) = 3/4
Sekarang kita dapat menjumlahkan pecahan tersebut:
- (2/4) + (3/4) = 5/4
Jadi, hasil penjumlahan 2_1/2 dan 3/4 adalah 2_5/4.
Contoh Soal 10: Perkalian Campuran Pecahan dan Bilangan Bulat
Hitung hasil dari perkalian berikut:
- 3_1/2 * 2
Solusi Soal 10: Dalam hal ini, kita perlu mengalikan bilangan bulat dan pecahan campuran terlebih dahulu, kemudian mengalikan hasilnya dengan bilangan bulat.
- Bilangan bulat: 3 * 2 = 6
- Pecahan campuran: 1/2
Kemudian, kita hanya perlu mengalikan bilangan bulat dengan pecahan campuran:
- 6 * 1/2 = 6/2 = 3
Jadi, hasil perkalian 3_1/2 dan 2 adalah 3.
CONTOH SOAL PECAHAN CAMPURAN
Contoh Soal 1: Penjumlahan Pecahan Campuran
Hitung hasil dari penjumlahan pecahan campuran berikut:
- 2_3/4 + 1_1/2
Cara Penyelesaian Soal 1: Dalam kasus ini, kita perlu menjumlahkan bilangan bulat, pecahan campuran, dan pecahan campuran.
- Bilangan bulat: 2 + 1 = 3
- Pecahan campuran: 3/4 + 1/2
Untuk menjumlahkan pecahan campuran, kita perlu mencari penyebut yang sama, yang dalam hal ini adalah 4. Kemudian, kita menyesuaikan kedua pecahan campuran ke penyebut 4:
- (3/4) + (2/4) = 5/4
Sekarang, kita memiliki pecahan campuran 3_5/4. Untuk menyederhanakan pecahan ini, kita bisa membagi pembilang oleh penyebut:
- 5/4 ÷ 4/4 = 5/4 ÷ 1 = 5/4
Jadi, hasil penjumlahan 2_3/4 dan 1_1/2 adalah 3_5/4 atau dalam bentuk campuran yang lebih sederhana, 3_1/4.
Contoh Soal 2: Pengurangan Pecahan Campuran
Hitung hasil dari pengurangan pecahan campuran berikut:
- 5_1/3 – 3_2/5
Cara Penyelesaian Soal 2: Dalam kasus ini, kita perlu mengurangkan bilangan bulat, pecahan campuran, dan pecahan campuran.
- Bilangan bulat: 5 – 3 = 2
- Pecahan campuran: 1/3 – 2/5
Untuk mengurangkan pecahan campuran, kita perlu mencari penyebut yang sama, yang dalam hal ini adalah 15 (KPK dari 3 dan 5). Kemudian, kita menyesuaikan kedua pecahan campuran ke penyebut 15:
- (1/3) * (5/5) = 5/15
- (2/5) * (3/3) = 6/15
Sekarang, kita dapat mengurangkan pecahan tersebut:
- (5/15) – (6/15) = -1/15
Jadi, hasil pengurangan 5_1/3 dan 3_2/5 adalah 2_(-1/15) atau dalam bentuk campuran yang lebih sederhana, 1_14/15.
Contoh Soal 3: Perkalian Pecahan Campuran dan Bilangan Bulat
Hitung hasil dari perkalian pecahan campuran dan bilangan bulat berikut:
- 2_1/4 * 3
Cara Penyelesaian Soal 3: Dalam kasus ini, kita perlu mengalikan bilangan bulat dan pecahan campuran terlebih dahulu, kemudian mengalikan hasilnya dengan bilangan bulat.
- Bilangan bulat: 2 * 3 = 6
- Pecahan campuran: 1/4
Kemudian, kita hanya perlu mengalikan bilangan bulat dengan pecahan campuran:
- 6 * 1/4 = 6/4
Sekarang, kita bisa menyederhanakan pecahan ini dengan membagi pembilang dan penyebut oleh faktor bersama terbesar (FPB), yaitu 2:
- (6/4) ÷ 2 = 3/2
Jadi, hasil perkalian 2_1/4 dan 3 adalah 3/2 atau dalam bentuk campuran, 1_1/2.
Contoh Soal 4: Pembagian Pecahan Campuran
Hitung hasil dari pembagian pecahan campuran berikut:
- 4_3/5 ÷ 2
Cara Penyelesaian Soal 4: Dalam kasus ini, kita perlu membagi pecahan campuran dengan bilangan bulat.
- Pecahan campuran: 3/5
Untuk melakukan pembagian, kita hanya perlu mengalikan pecahan campuran dengan kebalikan (pembalik) dari bilangan bulat 2, yaitu 1/2:
- (4_3/5) ÷ 2 = (3/5) * (1/2)
Kemudian, kita cukup mengalikan pembilang dengan pembilang dan penyebut dengan penyebut:
- (3/5) * (1/2) = 3/10
Jadi, hasil pembagian 4_3/5 oleh 2 adalah 3/10.