Lambang matematika merupakan simbol-simbol yang digunakan untuk merepresentasikan konsep matematika dalam bentuk yang lebih mudah dipahami dan lebih ringkas. Dalam artikel ini, akan dibahas tentang berbagai lambang matematika, penggunaannya, dan pentingnya dalam studi matematika.
Pengertian Lambang Matematika
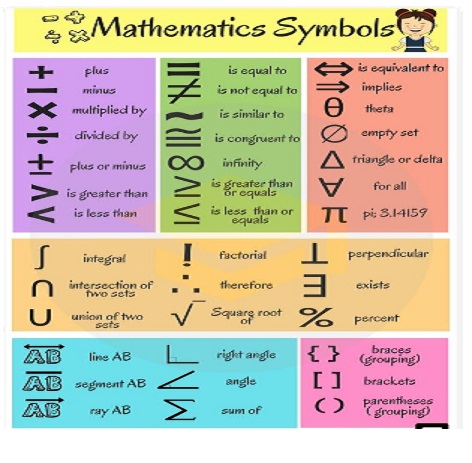
Lambang matematika adalah simbol atau notasi yang digunakan untuk merepresentasikan suatu konsep atau formula matematika. Lambang ini mempermudah dalam merepresentasikan dan menyajikan informasi matematika secara ringkas, sehingga lebih mudah untuk dipahami. Lambang matematika digunakan di berbagai bidang matematika, seperti aljabar, geometri, statistik, dan kalkulus.
Penggunaan Lambang Matematika
Lambang matematika digunakan di seluruh bidang matematika, mulai dari aritmatika dasar hingga kalkulus dan teori bilangan. Dalam aljabar, lambang matematika digunakan untuk merepresentasikan variabel, koefisien, dan konstanta. Lambang matematika juga digunakan dalam geometri untuk merepresentasikan sudut, garis, lingkaran, dan bentuk geometris lainnya. Selain itu, lambang matematika digunakan dalam kalkulus untuk merepresentasikan fungsi, integral, dan turunan.
Lambang matematika juga digunakan untuk merepresentasikan konsep matematika yang lebih kompleks, seperti bilangan kompleks, matriks, dan persamaan diferensial. Dalam statistik, lambang matematika digunakan untuk merepresentasikan distribusi probabilitas, ukuran kuantitatif, dan parameter statistik.
sejarah Lambang Matematika
Lambang-lambang matematika yang digunakan saat ini telah berkembang selama berabad-abad, dan beberapa di antaranya memiliki sejarah yang panjang dan berasal dari budaya yang berbeda-beda. Berikut adalah sejarah singkat dari beberapa lambang matematika yang paling umum:
- Angka dan bilangan: Angka dan bilangan telah digunakan sejak ribuan tahun yang lalu, dan banyak budaya kuno memiliki sistem bilangan mereka sendiri. Sistem bilangan Hindu-Arab yang digunakan saat ini di seluruh dunia berasal dari India pada abad ke-6.
- Tanda tambah dan kurang: Tanda tambah dan kurang pertama kali ditemukan dalam naskah matematika Arab pada abad ke-10.
- Tanda kali: Tanda kali pertama kali ditemukan pada abad ke-16 oleh seorang matematikawan Jerman bernama Johann Widman.
- Tanda sama dengan: Tanda sama dengan digunakan oleh matematikawan Inggris Robert Recorde pada tahun 1557.
- Tanda pembagian: Tanda pembagian awalnya ditemukan oleh matematikawan Skotlandia John Napier pada tahun 1617.
- Tanda persen: Tanda persen berasal dari kata Latin “per centum”, yang berarti “per seratus”. Tanda ini pertama kali digunakan pada abad ke-15.
- Tanda integral: Tanda integral pertama kali ditemukan oleh matematikawan Jerman Gottfried Wilhelm Leibniz pada abad ke-17.
- Tanda tak hingga: Tanda tak hingga pertama kali digunakan oleh matematikawan Inggris John Wallis pada abad ke-17.
- Tanda phi: Tanda phi berasal dari bahasa Yunani dan telah digunakan dalam matematika sejak zaman kuno.
- Tanda pi: Tanda pi telah digunakan selama berabad-abad dan berasal dari bahasa Yunani.
Contoh Lambang Bilangan
Lambang-lambang matematika terus berkembang seiring waktu, dan beberapa lambang baru telah ditambahkan ke dalam matematika modern. Hal ini menunjukkan betapa pentingnya lambang-lambang matematika dalam mempermudah komunikasi dan pemahaman konsep matematika.
Beberapa Lambang Matematika dan Penggunaannya
- “+” (tanda tambah): digunakan untuk menambahkan dua atau lebih angka atau variabel. Contoh: 2 + 3 = 5.
- “-” (tanda kurang): digunakan untuk mengurangkan dua atau lebih angka atau variabel. Contoh: 5 – 2 = 3.
- “x” (tanda kali): digunakan untuk mengalikan dua atau lebih angka atau variabel. Contoh: 2 x 3 = 6.
- “÷” (tanda bagi): digunakan untuk membagi dua atau lebih angka atau variabel. Contoh: 6 ÷ 2 = 3.
- “=” (tanda sama dengan): digunakan untuk menunjukkan bahwa dua nilai atau ekspresi matematika sama. Contoh: 2 + 3 = 5.
- “<” dan “>” (tanda kurang dari dan lebih dari): digunakan untuk membandingkan dua nilai atau ekspresi matematika. Contoh: 3 < 5 artinya 3 lebih kecil dari 5.
- “≤” dan “≥” (tanda kurang dari sama dengan dan lebih dari sama dengan): digunakan untuk membandingkan dua nilai atau ekspresi matematika yang sama atau lebih kecil/besar dari nilai lain. Contoh: 2 ≤ 5 artinya 2 kurang dari atau sama dengan 5.
- “≠” (tanda tidak sama dengan): digunakan untuk menunjukkan bahwa dua nilai atau ekspresi matematika tidak sama. Contoh: 2 ≠ 3 artinya 2 tidak sama dengan 3.
- “∑” (sigma): digunakan untuk menunjukkan penjumlahan dari suatu deret angka atau variabel. Contoh: ∑x menunjukkan penjumlahan dari semua nilai x dalam suatu deret.
- “∆” (delta): digunakan untuk menunjukkan perbedaan antara dua nilai atau variabel. Contoh: ∆x = x2 – x1 menunjukkan perbedaan antara x2 dan x1.
- “π” (pi): digunakan untuk merepresentasikan rasio keliling lingkaran dengan diameternya. Contoh: πr^2 menunjukkan luas lingkaran dengan jari-jari r.
- “∞” (infinity): digunakan untuk menunjukkan nilai yang tidak terbatas. Contoh: lim x → ∞ menunjukkan batas ketika x mendekati nilai tak terbatas.
- “∫” (integral): digunakan untuk menunjukkan operasi integrasi dalam kalkulus. Contoh: ∫f(x) dx menunjukkan integral dari fungsi f(x) terhadap variabel x.
- “∂” (partial): digunakan untuk menunjukkan turunan parsial dalam kalkulus. Contoh: ∂f(x,y) / ∂x menunjukkan turunan parsial dari fungsi f(x,y) terhadap variabel x.
- “√” (akar kuadrat): digunakan untuk menunjukkan akar kuadrat dari suatu angka atau variabel. Contoh: √25 = 5.
- “²” (pangkat dua): digunakan untuk menunjukkan suatu bilangan atau variabel dipangkatkan dua. Contoh: 3² = 9.
- “³” (pangkat tiga): digunakan untuk menunjukkan suatu bilangan atau variabel dipangkatkan tiga. Contoh: 2³ = 8.
- “⁻¹” (pangkat negatif satu): digunakan untuk menunjukkan invers dari suatu bilangan atau variabel yang dipangkatkan -1. Contoh: 4⁻¹ = 1/4.
- “!” (faktorial): digunakan untuk menunjukkan hasil dari operasi faktorial, yaitu perkalian semua bilangan asli dari 1 hingga n. Contoh: 5! = 5 x 4 x 3 x 2 x 1 = 120.
- “%” (persen): digunakan untuk menunjukkan perbandingan suatu angka dengan seratus. Contoh: 50% = 0,5.
- “∠” (sudut): digunakan untuk menunjukkan besaran sudut dalam geometri. Contoh: ∠ABC menunjukkan sudut di titik B dalam segitiga ABC.
- “|” (garis vertikal): digunakan untuk menunjukkan pembatas pada notasi matematika. Contoh: |x| menunjukkan nilai absolut dari x.
- “()” (tanda kurung): digunakan untuk menunjukkan urutan operasi dalam notasi matematika. Contoh: (2 + 3) x 4 menunjukkan operasi penjumlahan terlebih dahulu sebelum dikalikan dengan 4.
- “{}” (kurung kurawal): digunakan untuk menunjukkan himpunan dalam matematika. Contoh: {1, 2, 3} menunjukkan himpunan bilangan 1, 2, dan 3.
- “[]” (kurung siku): digunakan untuk menunjukkan matriks atau array dalam matematika. Contoh: [1 2; 3 4] menunjukkan matriks 2×2 dengan elemen 1, 2, 3, dan 4.
- “∩” (simbol irisan): digunakan untuk menunjukkan irisan antara dua himpunan. Contoh: A ∩ B menunjukkan himpunan yang terdiri dari elemen-elemen yang sama pada himpunan A dan B.
- “∪” (simbol gabungan): digunakan untuk menunjukkan gabungan antara dua himpunan. Contoh: A ∪ B menunjukkan himpunan yang terdiri dari elemen-elemen yang ada pada himpunan A atau B.
- “⊂” dan “⊃” (simbol subset dan superset): digunakan untuk menunjukkan bahwa suatu himpunan merupakan subhimpunan atau superhimpunan dari himpunan lain. Contoh: A ⊂ B menunjukkan bahwa himpunan A merupakan subhimpunan dari himpunan B.
- “∀” (simbol untuk semua): digunakan untuk menunjukkan kuantor universal, yaitu bahwa suatu pernyataan berlaku untuk semua elemen dalam suatu himpunan atau domain. Contoh: ∀x P(x) menunjukkan bahwa pernyataan P(x) berlaku untuk semua nilai x.
- “∃” (simbol ada): digunakan untuk menunjukkan kuantor eksistensial, yaitu bahwa suatu pernyataan benar untuk setidaknya satu elemen dalam suatu himpunan atau domain. Contoh: ∃x P(x) menunjukkan bahwa ada setidaknya satu nilai x yang membuat pernyataan P(x) benar.
- “→” (implikasi): digunakan untuk menunjukkan hubungan implikasi antara dua pernyataan. Contoh: jika P, maka Q dituliskan sebagai P → Q, yang berarti jika P benar, maka Q juga harus benar.
- “⇔” (if and only if): digunakan untuk menunjukkan hubungan logika yang saling mengikat antara dua pernyataan. Contoh: P ⇔ Q berarti P benar jika dan hanya jika Q benar.
- “∞” (tanda tak hingga): digunakan untuk menunjukkan konsep tak terbatas dalam matematika. Contoh: lim x → ∞ (1/x) = 0, yang berarti ketika x mendekati tak hingga, nilai 1/x mendekati nol.
- “≈” (kurang-lebih sama dengan): digunakan untuk menunjukkan kesamaan yang hampir sama dalam matematika. Contoh: π ≈ 3,14, yang berarti nilai π hampir sama dengan 3,14.
- “≥” dan “≤” (tanda lebih besar atau sama dengan dan tanda kurang besar atau sama dengan): digunakan untuk menunjukkan relasi perbandingan antara dua nilai. Contoh: 5 ≥ 3 dan 4 ≤ 6, yang berarti 5 lebih besar atau sama dengan 3 dan 4 kurang besar atau sama dengan 6.
- “≠” (tanda tidak sama dengan): digunakan untuk menunjukkan bahwa dua nilai tidak sama. Contoh: 4 ≠ 5, yang berarti bahwa nilai 4 tidak sama dengan nilai 5.
- “∑” (simbol sigma): digunakan untuk menunjukkan operasi penjumlahan dalam matematika. Contoh: ∑n dari n=1 hingga 5 sama dengan 1+2+3+4+5 = 15.
- “∫” (simbol integral): digunakan untuk menunjukkan operasi integral dalam matematika. Contoh: ∫f(x)dx menunjukkan integral dari fungsi f(x) terhadap variabel x.
- “∂” (simbol diferensial parsial): digunakan dalam kalkulus untuk menunjukkan turunan parsial. Contoh: ∂f/∂x menunjukkan turunan parsial dari fungsi f terhadap variabel x.
- “∇” (simbol nabla): digunakan dalam kalkulus untuk menunjukkan operator diferensial vektor. Contoh: ∇f menunjukkan gradien dari fungsi f.
- “×” (simbol perkalian silang): digunakan dalam kalkulus untuk menunjukkan perkalian silang antara dua vektor. Contoh: a × b menunjukkan hasil perkalian silang antara vektor a dan b.
- “∴” (simbol karena): digunakan untuk menunjukkan bahwa suatu pernyataan atau konklusi dapat disimpulkan dari premis yang diberikan. Contoh: A = B, B = C, ∴ A = C, yang berarti bahwa karena A sama dengan B dan B sama dengan C, maka A harus sama dengan C.
- “≡” (kongruen): digunakan dalam teori bilangan untuk menunjukkan bahwa dua bilangan memiliki sisa yang sama dalam mod n. Contoh: 10 ≡ 4 (mod 3) menunjukkan bahwa 10 dan 4 memiliki sisa yang sama ketika dibagi dengan 3.
- “∠” (simbol sudut): digunakan untuk menunjukkan sudut dalam geometri. Contoh: ∠ABC menunjukkan sudut di titik A dengan sisi AB dan BC sebagai sisinya.
- “°” (simbol derajat): digunakan untuk menunjukkan ukuran sudut dalam derajat. Contoh: ∠ABC = 90° menunjukkan bahwa sudut ABC memiliki ukuran 90 derajat.
- “∞” (simbol tak terbatas): digunakan untuk menunjukkan nilai yang tidak terbatas dalam matematika. Contoh: lim x → ∞ f(x) = ∞ menunjukkan bahwa nilai fungsi f(x) akan menjadi tak terbatas ketika x mendekati tak hingga.
- “Ø” (simbol kosong): digunakan untuk menunjukkan himpunan kosong dalam teori himpunan. Contoh: Himpunan kosong dinyatakan sebagai Ø.
- “∅” (simbol phi): sering digunakan untuk mewakili himpunan kosong dalam matematika.
- “⊥” (simbol garis tegak lurus): digunakan untuk menunjukkan relasi garis yang tegak lurus dalam geometri. Contoh: AB ⊥ CD menunjukkan bahwa garis AB tegak lurus terhadap garis CD.
- “∞” (simbol tak hingga): digunakan untuk menunjukkan nilai yang tidak terbatas dalam matematika. Contoh: lim x → ∞ f(x) = ∞ menunjukkan bahwa nilai fungsi f(x) akan menjadi tak terbatas ketika x mendekati tak hingga.