Pengertian Dimensi Besaran Penjelasan Fungsi Contoh – Dimensi sebuah besaran ialah penggambaran atau teknik penulisan sebuah besaran dengan memakai simbol atau emblem besaran pokok. Hal ini dapat diterangkan bahwa dimensi sebuah besaran menunjukkan teknik besaran tersebut tersusun dari besaran pokok.Apapun jenis satuan besaran yang dipakai tidak akan memprovokasi dimensi besaran tersebut.

Dimensi besaran diwakili dengan simbol, contohnya M, L, T yang mewakili massa (mass), panjang (length) dan masa-masa (time). Ada dua macam dimensi yakni Dimensi Primer dan Dimensi Sekunder. Dimensi Primer mencakup M (untuk satuan massa), L (untuk satuan panjang) dan T (untuk satuan waktu).

Dimensi Sekunder ialah dimensi dari seluruh Besaran Turunan yang ditetapkan dalam Dimensi Primer.

Contoh : Dimensi Gaya : M L T-2 atau dimensi Percepatan : L T-2.

Catatan :

Semua besaran fisis dalam mekanika dapat ditetapkan dengan tiga besaran pokok (Dimensi Primer) yakni panjang, massa dan waktu. Sebagaimana ada Satuan Besaran Turunan yang diturunkan dari Satuan Besaran Pokok, demikian pun ada Dimensi Primer dan Dimensi Sekunder yang diturunkan dari Dimensi Primer.

Pada sistem satuan internasional terdapat tujuh besaran pokok yang berdimensi dan dua besaran pokok ekstra tidak berdimensi. Adapun teknik untuk penulisan dimensi dari sebuah besaran ditetapkan dengan emblem huruf tertentu dan diberi kurung persegi. Hal ini dapat diterangkan dalam tabel di bawah ini

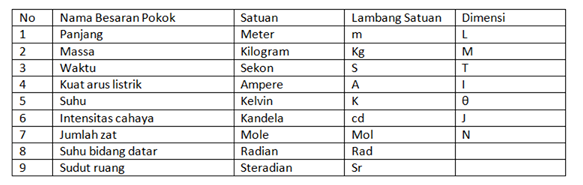
Dimensi dari besaran turunan dapat dibentuk dari dimensi besaran pokok yang dapat diterangkan sebagai berikut

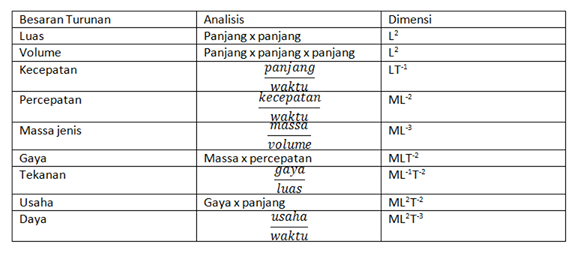
Masih tidak sedikit besaran turunan lainnya yang dapat diciptakan dimensinya. Ini dilaksanakan untuk memperlihatkan kebenaran dari besaran atau persamaan tersebut. Lebih lanjut, seiring dengan berjalannya waktu, pertumbuhan besaran turunan kian meningkat. Oleh karena itu, dapat disebutkan bahwa dimensi besaran turunan bisa terus diperbaharui.

Analisa Dimensional

Analisis dimensional merupakan analisis dimensi-dimensi besaran dan merupakan alat yang berguna dalam mekanika fluida modern.

Dalam suatu persamaan yang menunjukkan hubungan fisis antara besaran-besaran, harus ada kesamaan dimensional dan numerik yang mutlak. Pada umumnya, semua hubungan fisis seperti itu dapat disederhanakan menjadi besaran-besaran dasar yang terdiri dari gaya F, panjang L dan waktu T (atau massa M, panjang L dan waktu T). Kegunaan analisis dimensional antara lain :

1. Mengubah satu sistem satuan ke sistem satuan lain
2. Mengembangkan persamaan-persamaan
3. Mengurangi banyaknya variabel yang diperlukan dalam suatu percobaan
4. Menyatakan prinsip rancangan model

Contoh :

Nyatakan setiap besaran berikut (a) dalam suku-suku gaya F, panjang L dan waktu T dan (b) dalam suku-suku massa M, panjang L dan waktu T.

Jawab :

Fungsi Dimensi

1. Menunjukkan kesetaraan sejumlah besaran.
2. Dimensi dipakai untuk memperlihatkan kebenaran sebuah persamaan. Cara yang dapat dipakai untuk memperlihatkan kebenaran, salah satunya dengan analisa dimensional. Analisis dimensional merupakan teknik untuk menilai satuan dari sebuah besaran turunan. Ini dilaksanakan dengan teknik memperhatikan dimensi besaran tersebut. Manfaat dari konsep dimensi, salah satunya untuk meneliti atau mengulas benar atau salahnya sebuah persamaan atau faedah dimensi. Metode penjabaran dimensi atau analisis dimensi memakai aturan: (a) dimensi ruas kanan sama dengan dimensi ruas kiri dan (b) masing-masing suku berdimensi sama.
3. Dimensi dapat dipakai untuk menurunkan persamaan sebuah besaran dari besaran yang mempengaruhinya. Oleh seban itu, untuk memperlihatkan hukum fisika dapat dilaksanakan prediksi dari besaran yang mempengaruhinya. Dari besaran ini bisa ditentukan persamaan dengan memakai analisa dimensional. Di samping itu, hubungan antar besaran dari sebuah percobaan dapat ditindaklanjuti dengan analisa ini.

Contoh Soal

Contoh Soal 1

Tentukan dimensi besaran luas, kecepatan dan volume!

Penyelesaian:
Luas merupakan hasil kali panjang dan lebar, keduanya memiliki dimensi panjang [ L]
luas = panjang x lebar
[luas] = [panjang] [lebar]
[luas] = [ L] [ L] = [ L]2
Kecepatan merupakan hasil bagi jarak terhadap waktu. Dimensi jarak adalah [L], sedangkan waktu memiliki dimensi [ T ]. Jadi dimensi kecepatan adalah:
Kecepatan = jarak/waktu
[kecepatan] =[L]/[T] = [ L][ T ]-1
Volume adalah hasil kali panjang, lebar, dan tinggi. Ketiganya memiliki dimensi panjang [ L], sehingga dimensi volume adalah:
[volume] = [ panjang ] [ lebar] [tinggi]
[volume] = [ L] [ L] [ L] = [ L]3

Contoh Soal 2

Tentukan dimensi besaran berat jenis, momentum, dan energi potensial!

Penyelesaian:
Berat jenis merupakan hasil bagi berat dan volume, keduanya memiliki merupakan besaran turunan dan dapat dianalisis dimensinya. Untuk berat merupakan hasil perkalian antara massa dengan percepatan gravitasi yang dimensinya sama dengan dimensi percepatan yaitu [L][T]-2 maka dimensi berat adalah:
berat = massa x gravitasi
[berat] = [massa] [gravitasi]
[berat] = [M][L][T]-2
Sedangkan untuk volume memiliki dimensi [L]3, maka dimensi untuk berat jenis adalah:
berat jenis = berat/volume
[berat jenis] = [berat]/[volume]
[berat jenis] = [M][L][T]-2/[L]3
[berat jenis] = [M][L]-2[T]-2
luas = panjang x lebar
[luas] = [panjang] [lebar]
[luas] = [ L] [ L] = [ L]2
Kecepatan merupakan hasil bagi jarak terhadap waktu. Dimensi jarak adalah [L], sedangkan waktu memiliki dimensi [T]. Jadi dimensi kecepatan adalah
Kecepatan = jarak/waktu
[kecepatan] =[L]/[T] = [ L][ T ]-1
Volume adalah hasil kali panjang, lebar, dan tinggi. Ketiganya memiliki
dimensi panjang [ L], sehingga dimensi volume adalah:
[volume] = [ panjang ] [ lebar] [tinggi]
[volume] = [ L] [ L] [ L] = [ L]3
Momentum merupakan hasil perkalian antara massa dengan kecepatan, di mana massa memiliki dimensi [M] dan kecepatan merupakan hasil bagi antara perpindahan dengan waktu, sehingga dimensi kecepatan adalah [L][T]-1. Maka dimensi untuk momentum adalah:
momentum = massa x kecepatan
[momentum] = [massa][kecepatan]
[momentum] = [M][L][T]-1
Energi potensial merupakan hasil kali antara massa, percepatan gravitasi dan ketinggian. Di mana massa memiliki dimensi [M], percepatan gravitasi [L][T]-2 dan ketinggan memiliki dimensi [L], maka energi potensial memiliki dimensi:
energi potensial = massa x gravitasi x ketinggian
[energi potensial] = [massa][gravitasi][ketinggian]
[energi potensial] = [M][L][T]-2[L]
[energi potensial] = [M][L]2[T]-2