Pengertian Sudut Istimewa dan Tabel – Sudut istimewa adalah sudut dengan nilai perbandingan trigonometri yang dapat ditentukan nilainya tanpa menggunakan kalkulator. Sudut-sudut istimewa antara lain: 0°, 30°, 45°, 60°, 90°, dan seterusnya. Berikut ini merupakan nilai perbandingan trigonometri sudut-sudut istimewa tersebut. Pengertian dan definisi Trigonometri.

Trigonometri adalah bagian dari ilmu matematika yang mempelajari tentang hubungan antara sisi dan sudut suatu segitiga serta fungsi dasar yang muncul dari relasi tersebut. Trigonometri merupakan nilai perbandingan yang didefinisikan pada koordinat kartesius atau segitiga siku-siku.

Bagi para siswa, trigonometri identik dengan fungsi trigonometri yang meliputi sinus (sin), cosinus (cos), tangen (tan), cosecan (cosec), secan (sec), dan cotangen (cotan) yang kesemuanya merupakan cara untuk menentukan suatu sisi sebuah segitiga atau sudut yang terbentuk dari dua buah sisi dalam sebuah segitiga.

Trigonometri merupakan ilmu matematika yang sangat penting dalam kehidupan. Aplikasi ilmu trigonometri dalam kehidupan mencangkup segala bidang seperti astronomi, geografi, teori musik, elektronik, ekonomi, medical, teknik, dan masih banyak lagi. Dengan trigonometri kita bisa mengukur jarak suatu bintang diangkasa tanpa harus pergi kesana.

Dengan trigonometri kita bisa mengukur sudut ketinggian tebing tanpa harus memanjatnya. Bisa mengukur lebar suatu sungai tanpa harus menyeberanginya. Itulah manfaat dari mempelajari trigonometri dalam kehidupan sehari-hari. Trigonometri adalah sebuah konsep.

Hal pertama yang perlu dimengerti dalam memahami konsep dasar trigonometri adalah mengetahui, mengerti dan memahami bentuk dan rumus-rumus sebuah segitiga, terutama segitiga siku-siku. Pada dasarnya sebuah segitiga selalu terdiri dari 3 sisi, yaitu  sisi miring, sisi samping, dan sisi depan.

Dan tiga buah sudut yaitu sudut tegak lurus, sudut depan dan sudut samping. Dimana jika di tambahkan jumlah sudut sebuah segitiga haruslah 180 derajat. Tujuan utama mempelajari trigonometri dalam ilmu matematika adalah untuk menemukan nilai sebuah sudut atau panjang sebuah sisi sebuah segitiga. Untuk tujuan tersebut diatas maka trigonometri memiliki 2 nilai fungsi, yaitu:

Nilai fungsi Trigonometri

• Nilai fungsi trigonometri unuk sudut istimewa

Sudut istimewa disini adalah sudut yang besarnya 0, 30, 45, 60, 90 derajat. Untuk menentukan nilai fungsi sudut istimewa digunakan konsep geometri.

• Nilai fungsi trigonometri untuk sudut lainnya

Untuk menentukan nilai fungsi trigonometri sudut tidak istimewa biasanya menggunakan tabel atau scientific kalkulator yang dilengkapi dengan fungsi trigonometri.

Identitas Trigonometri

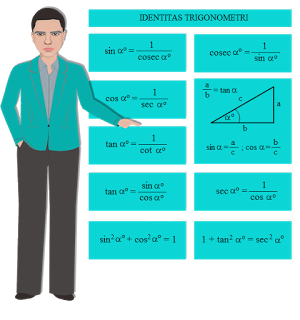
Dari nilai fungsi trigonometri tersebut kemudian diperoleh identitas trigonometri. Identitas trigonometri adalah suatu persamaan dari fungsi trigonometri yang bernilai benar untuk setiap sudutnya dengan kedua sisi ruasnya terdefinisi. Identitas trigonometri terbagi 3, yaitu Identitas Kebalikan, Identitas Perbandingan dan Identitas Phytagoras yang masing-masing memiliki fungsi dasar, yaitu:

 

Identitas Kebalikan	Identitas Perbandingan	Identitas Phytagoras
Cosec A = 1/ sin A Sec A = 1/cos A Cot A = 1/ tan A	Tan A = Sin A/ Cos A Cot A = Cos A / Sin A	Cos2 A + Sin2 A = 1 1 + tan2 A = Sec2 A 1 + Cot2 A = Cosec2 A

Fungsi trigonometri diatas dapat di proyeksikan kedalam sebuah grafik. Grafik fungsi trigonometri digunakan untuk mendeskripsikan fenomena alam seperti gerak gelombang, gerak harmonik sederhana, dan fenomena kelistrikan. Grafik fungsi trigonometri meliputi: grafik sinus, grafik cosinus dan grafik tangen.

MACAM –MACAM SUDUT ISTIMEWA

Sudut (90 – a)sin (90 – a) = Cos a Cos (90 – a) = sin a tan (90 – a) = cot a	Sudut (90 + a)sin (90 + a) = Cos a Cos (90 + a) = – sin a tan (90 + a) = – cot a
Sudut (180 – a)sin (180 – a) = sin a Cos (180 – a) = – Cos a tan (180 – a) = – tan a	Sudut (180 + a)sin (180+a) = -sina Cos (180 + a) = – Cos a tan (180 + a) = tan a
Sudut (270 – a)sin (270 – a) = – Cos a cos (270 – a) = – sin a tan (270 – a) = ctg a	Sudut (270 + a)sin (270 + a) = -cos a cos (270 + a) = sin a tan (270 + a) = – cot a
Sudut (360 – a)sin (360 – a) = – sin a Cos (360 – a) = Cos a tan (360 – a) = – tan a	Sudut (360 + a)sin (360 + a) = sin a Cos (360 + a) = Cos a tan (360 + a) = tan a

Sudut Negatif sin (-a)  = – sin a

Cos (-a) = Cos a

tan (-a) = – tan a

Sudut negatif dihitung searah dengan jarum jam.Tanda pada sudut negatif sesuai dengan tanda pada kuadran ke IV.Keterangan :

Untuk a sudut lancip

Kuadran	Hubungan
I	a	atau	(90 – a)
II	(180 – a)		(90 + a)
III	(180 + a)		(270 – a)
IV	(360 – a)		(270 + a)

Tabel Nilai Trigonometri Sudut Istimewa

Pada tabel di bawah ini, perhatikan bahwa nilai sinus dimulai dari 0 menjadi 1 dan kembali lagi ke 0. Sebaliknya, nilai cosinus dimulai dari 1 menjadi 0 dan kembali ke 1 begitu seterusnya. Lihat bahwa beberapa sudut memiliki nilai sinus atau cosinus yang sama tapi sebagian berbeda tanda yaitu ada yang positif dan ada yang negatif. Nah untuk menentukan positif atau negatif, maka gunakanlah konsep kuadran yang telah dijelaskan di atas.

–	0o	30o	45o	60o	90o	120o	135o	150o	180o
sin	0	½	½√2	½√3	1	½√3	½√2	½	0
cos	1	½√3	½√2	½	0	-½	-½√2	-½√3	-1
tan	0	1/3√3	1	√3	–	-√3	-1	-1/3√3	0

 

–	210o	225o	240o	270o	300o	315o	330o	360o
sin	-½	-½√2	-½√3	-1	-½√3	-½√2	-½	0
cos	-½√3	-½√2	-½	0	½	½√2	½√3	1
tan	1/3√3	1	√3	–	-√3	-1	-1/3√3	0

Nah, di atas adalah tabel nilai perbandingan trigonometri sudut istimewa. Karena jumlahnya tidak sedikit, maka sebenarnya kita cukup menghafal sudut 0o – 90o saja. Selebihnya, kita dapat mengikuti pola tabel di atas. Untuk lebih jelasnya perhatikan contoh berikut :

Anggaplah anda sudah hafal nilai trigonometri untuk sudut 0o – 90o. Lalu anda diminta untuk menentukan nilai sin 150o, dan cos 135o. Sebenarnya ada dua trik untuk menjawab soal ini yaitu :

Anda harus hafal sudut-sudut apa saja yang istimewa dan bagaimana polanya.Perhatikan tabel di atas! Anggaplah mereka sebagai suatu barisan dengan pola yaitu diawali dari 0 kemudian ditambah 30, ditambah 15, dan ditambah 30 lagi sampai sudut 90o. Untuk sudut selanjutnya, pola tersebut berulang sampai ke sudut 360o. Nah, pada soal kita diminta untuk menentukan nilai sin 150o, dan cos 135o. Jika anda sudah hafal sudut-sudut istimewa, maka anda akan tahu bahwa sudut 150o berada di sebelah sudut 135o. Anda dapat membuat coretan kecil jika belum terlalu hafal. Tulis barisan sudut istimewa sebagai berikut :

0o

30o

45o

60o

90o

120o

135o

150o

Selanjutnya, anda harus hafal pola nilai trigonometri seperti yang terlihat pada tabel yaitu :
⇒ Untuk sinus = 0 − ½ − ½√2 − ½√3 − 1 − ½√3 − ½√2 − ½ − 0.
⇒ Untuk cosinus = 1 − ½√3 − ½√2 − ½ − 0 − ½ − ½√2 − ½√3 − 1.

–	0o	30o	45o	60o	90o	120o	135o	150o
sin	0	½	½√2	½√3	1	½√3	½√2	½
cos	1	½√3	½√2	½	0	-½	-½√2	-½√3

Nah, berdasarkan tabel yang sudah kita buat, maka jelas terlihat bahwa :

sin 150o = ½

cos 135o = -½√2

terbiasa dengan pola itu maka anda akan langsung tahu nilainya tanpa harus membuat coretan terlebih dahulu.

Tahap awal memang terkesan masih rumit, tapi percayalah jika anda sudah

Anda harus faham konsep relasi sudut antar kuadran
Pada artikel sebelumnya telah dibahas rumus pebandingan trigonometri untuk sudut-sudut berelasi. Hanya ada beberapa aturan yang harus diingat yaitu :

⇒ Untuk sudut (90  ± a) dan (270 ± a) berlaku : sin = cos, cos = sin,
tan = cot, cot = tan, sec = cosec, cosec = sec ; dengan tanda positif
dan negatif disesuaikan berdasarkan ASTC.

⇒ Untuk sudut (180 ± a) dan (360 ± a) berlaku : sin = sin, cos = cos,
tan = tan, cot = cot, sec = sec, cosec = cosec ; dengan tanda positif
dan negatif disesuaikan berdasarkan ASTC.Sekarang kembali ke soal.
sin 150o = sin (90 + 60)

⇒ sin 150o  = cos 60

⇒ sin 150o  = ½
Keterangan : sudut 150o berada pada kuadran II (hanya sinus dan cosecan yang positif), jadi sin 150o bernilai positif. Tanda sin berubah jadi cos karena kita menggunakan operator (90 + a).cos 135o = cos (180 – 45)

⇒ cos 135o = – cos 45

⇒ cos 135o = -½√2.

Keterangan : sudut 135o berada pada kuadran II (hanya sinus dan cosecan yang positif), jadi cos 135o bernilai negatif. Tanda cos tetap jadi cos karena kita menggunakan operator (180 – a).Kalau kita menggunakan rumus (90 + a) untuk soal no 2, maka :
cos 135o = cos (90 + 45)

⇒ cos 135o = – sin 45

⇒ cos 135o = -½√2.

Keterangan : sudut 135o berada pada kuadran II (hanya sinus dan cosecan yang positif), jadi cos 135o bernilai negatif. Tanda cos berubah jadi sin karena kita menggunakan operator (90 + a).